Traders, as Gregas e
Gestão de Risco
HOW TRADERS MANAGE THEIR RISKS
The trading function within a financial institution is referred to as the front office. The part of the financial institution that is concerned with the overall level of the risks being taken, capital adequacy, and regulatory compliance is referred to as the middle office. The record keeping function is referred to as the back office. As explained in Section 1.6, there are two levels within a financial institution at which trading risks are managed. First, the front office hedges risks by ensuring that exposures to individual market variables are not too great. Second, the middle office aggregates the exposures of all traders to determine whether the total risk is acceptable. In this chapter we focus on the hedging activities of the front office. In later chapters we will consider how risks are aggregated in the middle office.
This chapter explains what are termed the “Greek letters” or simply the “Greeks.” Each of the Greeks measures a different aspect of the risk in a trading position. Traders calculate their Greeks at the end of each day and are required to take action if the internal risk limits of the financial institution they work for are exceeded. Failure to take this action is liable to lead to immediate dismissal.
"Chapter 8. - How Traders Manage Their Risks" do livro do John C. Hull, “Risk Management and Financial Institutions”, 5th Edition, Wiley Finance Series, 2018.
AS GREGAS !
A financial institution that sells an option to a client in the over-the-counter markets is faced with the problem of managing its risk. If the option happens to be the same as one that is traded actively on an exchange or in the OTC market, the financial institution can neutralize its exposure by buying the same option as it has sold. But when the option has been tailored to the needs of a client and does not correspond to the standardized products traded by exchanges, hedging the exposure is far more difficult.
Most traders use more sophisticated hedging procedures than those mentioned so far. These hedging procedures involve calculating measures such as delta, gamma, and vega. The measures are collectively referred to as Greek letters. They quantify different aspects of the risk in an option position. This chapter considers the properties of some of most important Greek letters.
In order to calculate a Greek letter, it is necessary to assume an option pricing model. Traders usually assume the Black–Scholes–Merton model (or its extensions in Chapters 17 and 18) for European options and the binomial tree model (introduced in Chapter 13) for American options. (As has been pointed out, the latter makes the same assumptions as Black–Scholes–Merton model.) When calculating Greek letters, traders normally set the volatility equal to the current implied volatility. This approach, which is sometimes referred to as using the ‘‘practitioner Black–Scholes model,’’ is appealing.
"Chapter 19. - The Greek Letters", do livro do John C. Hull, “Options, Futures, and Other Derivatives”, 10th Edition, Publisher: Pearson, 2018.
GREEK LETTERS CALCULATED USING MONTE CARLO SIMULATION

"Section 21.6 - Monte Carlo Simulation", "Chapter 21. - Basic Numerical Procedures", do livro do John C. Hull, “Options, Futures, and Other Derivatives”, 10th Edition, Publisher: Pearson, 2018.


Aron Gottesman, “Derivatives Essentials: An Introduction to Forwards, Futures, Options and Swaps”, Wiley Finance, 2016.
DELTA and GAMMA
Imagine that you are a trader working for a U.S. bank and are responsible for all trades involving gold. The current price of gold is $1,300 per ounce. Table 8.1 shows a summary of your portfolio (known as your “book”).
How can you manage your risks?

obs: Considere que a Tabela 8.1 é valorada no final do dia com "marcação à mercado".
The value of your portfolio is currently -$5,683,000. (This could be partly because you have been a net seller of options and partly because the market has moved against you.) One way of investigating the risks you face is to revalue the portfolio on the assumption that there is a small increase in the price of gold from $1,300 per ounce to $1,300.10 per ounce. Suppose that this $0.10 increase in the price of gold decreases the value of your portfolio by $100 from -$5,683,000 to -$5,683,100. This means that the sensitivity of the portfolio to the price of gold is
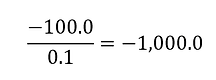
This is referred to as the delta of the portfolio. The portfolio loses value at a rate of about $1,000 per $1 increase in the price of gold. Similarly, it gains value at a rate of about $1,000 per $1 decrease in the price of gold.
In general, the delta of a portfolio with respect to a market variable is

Where ΔS is a small increase in the value of the variable and ΔP is the resulting change in the value of the portfolio. Using calculus terminology, delta is the partial derivative of the portfolio value with respect to the value of the variable:
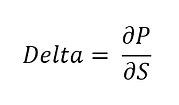
In our example, the trader can eliminate the delta exposure by buying 1,000 ounces of gold .This is because the delta of a long position in 1,000 ounces of gold is 1,000.(The position gains value at the rate of $1,000 per $1 increase in the price of gold.) This is known as delta hedging. When the hedging trade is combined with the existing portfolio the resultant portfolio has a delta of zero. Such a portfolio is referred to as delta neutral.
Options and other more complex derivatives dependent on the price of an underlying asset are nonlinear products. The relationship between the value of the product and the underlying asset price at any given time is nonlinear. This nonlinearity makes them more difficult to hedge for two reasons. First, making a nonlinear portfolio delta neutral only protects against small movements in the price of the underlying asset. Second, we are not in a hedge-and-forget situation. The hedge needs to be changed frequently. This is known as dynamic hedging.
The gamma, Γ, of a portfolio measures the extent to which large changes cause problems. Gamma is the rate of change of the portfolio’s delta with respect to the price of the underlying asset. It is the second partial derivative of the portfolio with respect to asset price:
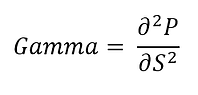
If gamma (Γ) is small, delta (Δ) changes slowly, and adjustments to keep a portfolio delta neutral need to be made only relatively infrequently. However, if gamma is large in absolute terms, delta is highly sensitive to the price of the underlying asset. It is then quite risky to leave a delta-neutral portfolio unchanged for any length of time.
Making a Portfolio Gamma Neutral
A linear product has zero gamma and cannot be used to change the gamma of a portfolio. What is required is a position in an instrument, such as an option, that is not linearly dependent on the underlying asset price.
"Chapter 8. - How Traders Manage Their Risks" do livro do John C. Hull, “Risk Management and Financial Institutions”, 5th Edition, Wiley Finance Series, 2018.
